Studying Racemization Using DFT and Identity Reactions
In this section, I’ll walk you through how I use Density Functional Theory (DFT) and the concept of identity reactions to computationally understand racemization. The data is based on the published paper titled “Sulfur–Phenolate Exchange: SuFEx-Derived Dynamic Covalent Reactions and Degradation of SuFEx Polymers”.
We’ll compare the activation barriers of a desired stereospecific reaction (SuPhenEx) against a competing, undesired pathway (an identity reaction) that leads to racemization, resulting in loss of enantiospecificity (es) in some of the phenolates with electron-withdrawing groups (EWGs).
Step 1: SuPhenEx Activation Barriers (ΔH‡)
The table below shows the calculated activation enthalpies (ΔH‡) for SuPhenEx reactions with different substituents:
| Substituent (R) | ΔH‡ [kcal/mol] | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p-OMe | 9.6 | |||||||||||
| p-H | 11.6 | |||||||||||
| p-CN | 19.3 |
As the substituent becomes more electron-withdrawing, the ΔH‡ increases, indicating that the SuPhenEx reaction becomes slower.
Step 2: Identity Reaction (Racemization Pathway)
To understand how racemization occurs, I model identity reactions, where a product molecule exchanges phenolates with itself. This results in stereochemical scrambling without any net change in structure.
How I Set Up Identity Reactions in DFT:
- Use the product structure (e.g.,
para-Nitro-phenolate) as the starting geometry. - Construct a symmetric transition state, where the leaving and entering phenolates are equidistant. Refer image
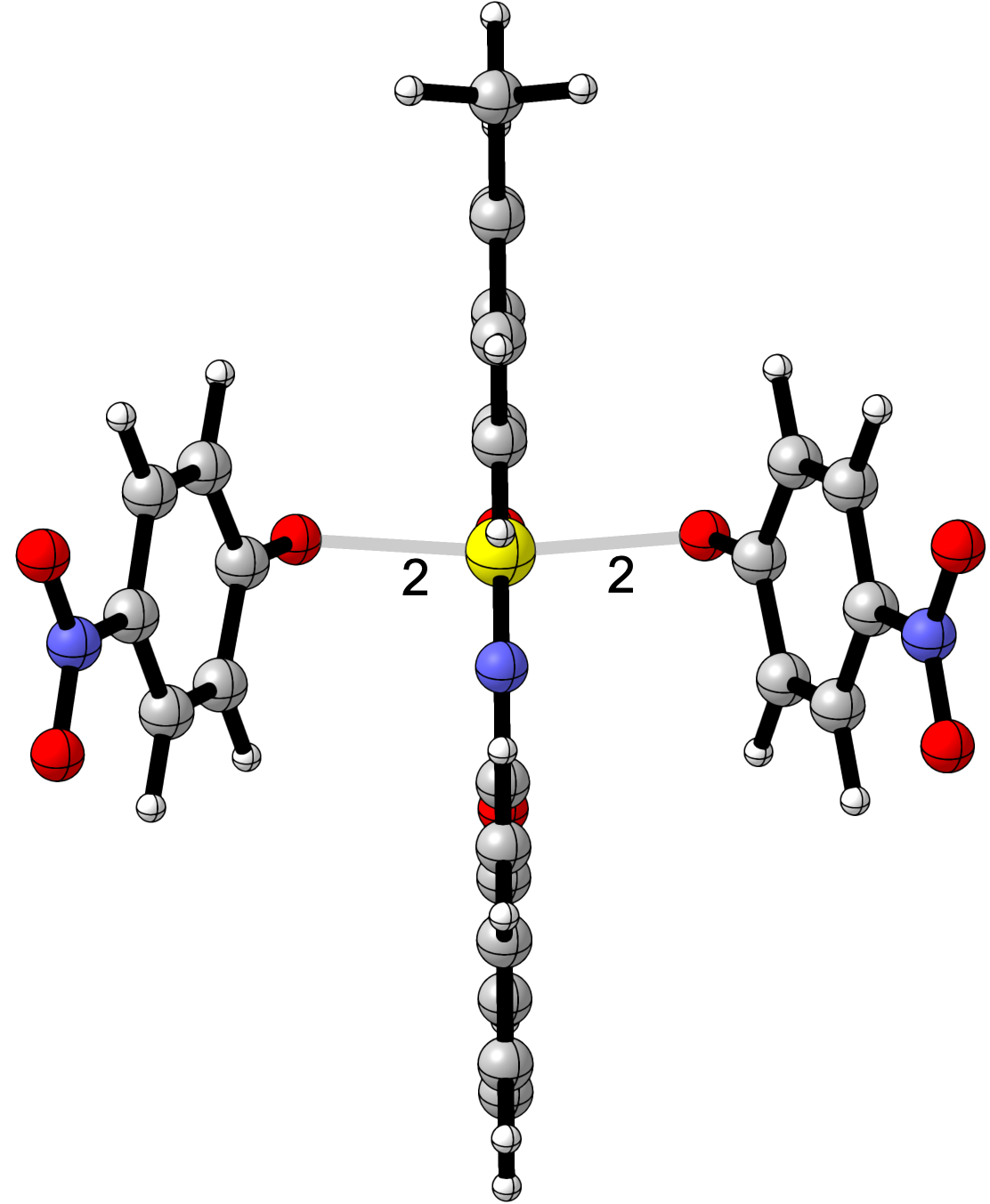
- Adjust bond distances and angles to create a mirror-symmetric geometry.
- Optimize using a suitable DFT method (e.g.,
B3LYP-D3(BJ)/def2-TZVP) with solvation if needed.
Here are the calculated activation barriers for identity reactions:
| Substituent (R) | ΔH‡ [kcal/mol] | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p-OMe | 19.3 | |||||||||||
| p-H | 19.4 | |||||||||||
| p-CN | 20.9 | |||||||||||
| p-NO₂ | 22.4 |
These ΔH‡ values are consistently higher than those for SuPhenEx, but the gap narrows with EWGs.
Step 3: Interpreting ΔΔH‡ — The Selectivity Indicator
To assess how likely racemization is, I compute:
ΔΔH‡ = ΔH‡(identity) − ΔH‡(SuPhenEx)
| Substituent (R) | ΔΔH‡ [kcal/mol] | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p-OMe | 9.7 | |||||||||||
| p-H | 7.8 | |||||||||||
| p-CN | 1.6 |
Low ΔΔH‡ values (e.g., p-CN i.e.,
(S)-3k) imply that the racemization pathway is energetically competitive with SuPhenEx, explaining why enantiospecificity breaks down in these cases. This also suggests starting with a leaving group containing p-NO₂ is useful in avoiding the racemization as the identity reaction barrier for p-NO₂ is the highest among the substituents.
Summary
- DFT allows me to quantify racemization potential by comparing the ΔH‡ of SuPhenEx and identity pathways.
- Symmetrizing the product is essential to locating the racemization transition state.
- ΔΔH‡ gives a clear metric for stereochemical robustness.
This computational approach helps explain experimental results and serves as a predictive guide for designing more robust enantiospecific reactions.